ツクールVX製のフリー短編連載RPGを公開しています。 現在Ⅱ章まで公開中。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
皆さん今日は、Alhenaです。
年の瀬も迫って参りましたが、恙無く過ごされていらっしゃいますでしょうか。
最後まで気を抜かず、息災でいたいものですね。
先日大学の図書館を徘徊していたら、日本の名字図鑑なるものを発見しました。
少し中を覗いてみると中二心を擽られる単語がごろごろしていて、あっという間に数十分が経過していきました。
中々侮れないません。
小説の中でだけ見たような奇異な名字も多数掲載されており、西澤保彦辺りは執筆するたびにこの手のものを参考にしているのではないかと邪推します。
案外日本は広いものですね。
そんなわけで3章がまだ出来てないというのにも拘らず、新キャラの名前が先に決まってしまいました。
当然和名なので、ある程度特別な意味を持たせたい、なんてことを考えていたらキャラ付けもそこそこ纏まって、ついでに4章の構想まで半ば固まって来ました。
そろそろ大きく前進する時が来たのかもしれません。
暑い暑いと言って進まなかった作業は暑くなくなってもやはり進みませんでしたが、ここにきて天啓が舞い降りてきたような気がします。
願わくは気の所為に終わらないことを期待します。
最後にAbleへ一言。
彼には此処とは無関係の所で書いている日誌があるのですが……彼はツクールXPとVXで何を見てきたのでしょうか。
年の瀬も迫って参りましたが、恙無く過ごされていらっしゃいますでしょうか。
最後まで気を抜かず、息災でいたいものですね。
先日大学の図書館を徘徊していたら、日本の名字図鑑なるものを発見しました。
少し中を覗いてみると中二心を擽られる単語がごろごろしていて、あっという間に数十分が経過していきました。
中々侮れないません。
小説の中でだけ見たような奇異な名字も多数掲載されており、西澤保彦辺りは執筆するたびにこの手のものを参考にしているのではないかと邪推します。
案外日本は広いものですね。
そんなわけで3章がまだ出来てないというのにも拘らず、新キャラの名前が先に決まってしまいました。
当然和名なので、ある程度特別な意味を持たせたい、なんてことを考えていたらキャラ付けもそこそこ纏まって、ついでに4章の構想まで半ば固まって来ました。
そろそろ大きく前進する時が来たのかもしれません。
暑い暑いと言って進まなかった作業は暑くなくなってもやはり進みませんでしたが、ここにきて天啓が舞い降りてきたような気がします。
願わくは気の所為に終わらないことを期待します。
最後にAbleへ一言。
彼には此処とは無関係の所で書いている日誌があるのですが……彼はツクールXPとVXで何を見てきたのでしょうか。
PR
先日の嵐で秋も愈々終焉の様相を呈してきました。
週明けにはMLBのウィンターミーティングも始まりますし、私の最も好きな季節になろうとしています。
唯一の不満は野球がオフシーズンであることですが、youtubeのMLBチャンネルやMVPベースボールなどで無聊を慰めています。
皆さん今日は、Alhenaです。
先日今年の本屋大賞に選ばれた『天地明察』を友達に薦められたので読んでみました。
小説自体も流石に噂に違わぬ面白さだったのですが、私が注目したいのは例によって作中の問題についてです。
長さを長さで割っても面積を面積で割っても長さになるような明らかにおかしい誤問や、条件の通りに平均を出すとどう考えても絵に合わなくなる招差術の問題はどうでもいいのですが、気になったのは冒頭に登場する三角形と円の問題です。
先ずは問題を掲載しておきます。

上図のように直角三角形の中に直径の等しい二つの円が接している。
釣9寸、股12寸の時、円の直径を求めよ。
手元に本が無いので問題文は適当ですが、設問自体には影響ない筈です。
この問題を解くのに主人公は結構な苦労を強いられるのですが、実際解いてみるとさほど難しいとは感じないと思います。
ただし、小説の後半で登場人物の一人が代数を生みだしたという記述があるので、江戸時代初期当時の算術を考えればかなりの難問だったのかもしれません。
それは兎も角、この問題に対して主人公の出した答えは以下のようなものでした。
{2*釣*股/(釣+股+勾)}*{勾/(釣+股)}
この問題を初めて解いた時に、この式と一致する解法を採った方はいらっしゃるのでしょうか。
私の周囲では私を含め4人ほどこの問題に挑みましたが、皆この式で表される解法にはなりませんでした。
皆さんも是非試してみて下さい。
なのでどのような解法ならば過不足なくこの式に行き当たるかを私なりに考えてみました。
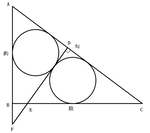
上図のように釣を延長し、二つの円の接点を通り勾に垂直な直線を引きます。
この時、⊿ADFと⊿EDCは、共に⊿ABCと相似なので相似であり、同じ半径の内接円を持っている為、合同になります。
従ってAD=EDですから、⊿ABCと⊿EDCの相似比は、
AB+BC : ED+DC = AB+BC : AD+DC = AB+BC : AC となります。
ここで、⊿ABCの内接円の直径を考えると、2*{AB*BC/(AB+BC+CA)} ですから、答え、即ち⊿EDCの内接円の直径は次式で表されます。
{2*AB*BC/(AB+BC+CA)}*{AC/(AB+BC)}
一部形を合わせる為に手は加えていますが、これで主人公の式と一致しました。
彼の辿った解法はこのようなものだったのではないかと想像します。
以上、下らない妄想にお付き合い頂き有難う御座いました。
週明けにはMLBのウィンターミーティングも始まりますし、私の最も好きな季節になろうとしています。
唯一の不満は野球がオフシーズンであることですが、youtubeのMLBチャンネルやMVPベースボールなどで無聊を慰めています。
皆さん今日は、Alhenaです。
先日今年の本屋大賞に選ばれた『天地明察』を友達に薦められたので読んでみました。
小説自体も流石に噂に違わぬ面白さだったのですが、私が注目したいのは例によって作中の問題についてです。
長さを長さで割っても面積を面積で割っても長さになるような明らかにおかしい誤問や、条件の通りに平均を出すとどう考えても絵に合わなくなる招差術の問題はどうでもいいのですが、気になったのは冒頭に登場する三角形と円の問題です。
先ずは問題を掲載しておきます。
上図のように直角三角形の中に直径の等しい二つの円が接している。
釣9寸、股12寸の時、円の直径を求めよ。
手元に本が無いので問題文は適当ですが、設問自体には影響ない筈です。
この問題を解くのに主人公は結構な苦労を強いられるのですが、実際解いてみるとさほど難しいとは感じないと思います。
ただし、小説の後半で登場人物の一人が代数を生みだしたという記述があるので、江戸時代初期当時の算術を考えればかなりの難問だったのかもしれません。
それは兎も角、この問題に対して主人公の出した答えは以下のようなものでした。
{2*釣*股/(釣+股+勾)}*{勾/(釣+股)}
この問題を初めて解いた時に、この式と一致する解法を採った方はいらっしゃるのでしょうか。
私の周囲では私を含め4人ほどこの問題に挑みましたが、皆この式で表される解法にはなりませんでした。
皆さんも是非試してみて下さい。
なのでどのような解法ならば過不足なくこの式に行き当たるかを私なりに考えてみました。
上図のように釣を延長し、二つの円の接点を通り勾に垂直な直線を引きます。
この時、⊿ADFと⊿EDCは、共に⊿ABCと相似なので相似であり、同じ半径の内接円を持っている為、合同になります。
従ってAD=EDですから、⊿ABCと⊿EDCの相似比は、
AB+BC : ED+DC = AB+BC : AD+DC = AB+BC : AC となります。
ここで、⊿ABCの内接円の直径を考えると、2*{AB*BC/(AB+BC+CA)} ですから、答え、即ち⊿EDCの内接円の直径は次式で表されます。
{2*AB*BC/(AB+BC+CA)}*{AC/(AB+BC)}
一部形を合わせる為に手は加えていますが、これで主人公の式と一致しました。
彼の辿った解法はこのようなものだったのではないかと想像します。
以上、下らない妄想にお付き合い頂き有難う御座いました。
皆さん今日は、Alhenaです。
以前本ブログで軽く紹介した、KCのBullingtonがまさかの広島入りだそうです。
今シーズン殆ど良い所の無かったBullingtonですが、8月半ばの対NYY戦での快投が忘れられない私としてはもう一年KCで見たかった思いが強いです。
まあ決まってしまったことは仕方ないので、広島での活躍に期待しましょう。
移籍先がNPBならば安心して応援できますしね。
そんなこんなでWMに向けてストーブリーグも盛り上がってきた昨今、皆様いかがお過ごしでしょうか。
色々と流行性のウィルスが蔓延しそうな噂も聞きますが、健康に年末を迎えたいものです。
話は変わりますが、最近エコポイントの駆け込み需要とやらでテレビの販売台数が増加しているそうですね。
それを見たある人が、テレビに映る内容が変わるわけでもないのに買い替える必要性なんてあるのか、という発言をしているのを小耳に挟みました。
私の自宅には10年以上前に買ったブラウン管のテレビしかないのですが、そう言われるとテレビ局の流す映像を見ていて、テレビに対して不満を感じたことは殆ど無いように思えます。
不満を最も感じたのはFF13のプレイ中にやたら字が読みにくいことなのですが、これならばテレビではなくPCモニターでも買えば事足ります。
そう思ってPC用のモニターとテレビの値段を比較してみると、テレビの値段は異様なまでに高いように感じられます。
特に私の家の場合はケーブルテレビと契約しているので、ますますテレビであることの意義は薄れます。
そもそもエコポイントは今までも有ったのに買っていなかったという事実が、不必要性の証明のような気もしますが……。
以前本ブログで軽く紹介した、KCのBullingtonがまさかの広島入りだそうです。
今シーズン殆ど良い所の無かったBullingtonですが、8月半ばの対NYY戦での快投が忘れられない私としてはもう一年KCで見たかった思いが強いです。
まあ決まってしまったことは仕方ないので、広島での活躍に期待しましょう。
移籍先がNPBならば安心して応援できますしね。
そんなこんなでWMに向けてストーブリーグも盛り上がってきた昨今、皆様いかがお過ごしでしょうか。
色々と流行性のウィルスが蔓延しそうな噂も聞きますが、健康に年末を迎えたいものです。
話は変わりますが、最近エコポイントの駆け込み需要とやらでテレビの販売台数が増加しているそうですね。
それを見たある人が、テレビに映る内容が変わるわけでもないのに買い替える必要性なんてあるのか、という発言をしているのを小耳に挟みました。
私の自宅には10年以上前に買ったブラウン管のテレビしかないのですが、そう言われるとテレビ局の流す映像を見ていて、テレビに対して不満を感じたことは殆ど無いように思えます。
不満を最も感じたのはFF13のプレイ中にやたら字が読みにくいことなのですが、これならばテレビではなくPCモニターでも買えば事足ります。
そう思ってPC用のモニターとテレビの値段を比較してみると、テレビの値段は異様なまでに高いように感じられます。
特に私の家の場合はケーブルテレビと契約しているので、ますますテレビであることの意義は薄れます。
そもそもエコポイントは今までも有ったのに買っていなかったという事実が、不必要性の証明のような気もしますが……。
皆さん今日は、Alhenaです。
何時の間にか11月ももう下旬に入ろうとしていますが、如何お過ごしでしょうか。
……9月にⅢ章いけるかも、なんて言っていたのがつい昨日のことのように思えます。光陰矢のごとしとは良く言ったものですね。
いい加減充電期間も終わらせなければ。
さて、今日の話題は3回前に投稿したビリヤードの玉の問題についてです。
皆さん解けましたか?
以下一部解法に触れますので、自力で解きたい方はご注意ください。
一先ず問題を再掲しておきます。
『五つのビリヤードの玉を、真珠のネックレスのように、リングにつなげてみるとしよう。玉には、それぞれナンバーが書いてあるな。さて、この五つの玉のうち、幾つ取っても良いが、隣どうし連続したものしか取れないとしよう。一つでも、二つでも、五つ全部でも良い。しかし、離れているものは取れない。この条件で取った玉のナンバーを足し合わせて、1から21までのすべての数ができるようにしたい。さあ、どのナンバーの玉をどのように並べて、ネックレスを作れば良いかな?』
(森博嗣『笑わない数学者』より抜粋)
この問題を考察する上での肝は、21という数字が何処から出てきたかということにあるのですが、此処を乗り越えてしまえば球の個数が5個の場合に限らず、n個の場合に拡張して考えることも比較的容易にできます。
そうは言っても答えが規則的に現れる訳ではないので、同じ考え方が使えると言うだけですが、同じ考え方が使えるということは、機械的に解法をプログラムできるということになります。
そんな訳で例によってRGSSで手慰みに書いてみたのですが、それを出す前に先ず21の持つ意味を説明しますと、これは5個の玉の取り方の数になります。
取る玉の数1~4個に対して、取り始める点が5か所ずつ、それに全て取った場合の1通りを加えて 4*5+1=21 通りですね。
n個に拡張した場合は n(n-1)+1 通りになります。
また、これは全ての取り方に於いて球の数の和に重複は存在しないことを示しています。
例えば1と2の玉が隣り合っていたら、3の玉は絶対に入りません。
更にこのことを考えれば、1~21の全ての数を作るという条件を、5つの玉の数の総和が21かつ全ての取り方に於いて和に重複が無い、と言い変えることができます。
こうすることで条件の一致不一致を素早く判別することができます。
以上のことを考察した上で解法をスクリプトにしてみました。興味のある方はご覧下さい。
billiards.txt
さて、これを使って計算してみると答えの個数について面白い事実が浮かび上がって来ます。
球の個数が4個の時に二つ答えが出るのは人が考えても直ぐに分かりますが、6個にすると答えは五つに増え、更に7個にすると今度は答えは存在しないのです。
球の個数が1個の時から答えの数を並べると
1→1→1→2→1→5→0→6→4→6→0→18→……
となります。
今ブログを書いているPC環境では、12個の場合を計算するのに3,4分掛かったので、これ以上は面倒で計算してませんが、こういった規則性の無さにも数字の醍醐味を感じますね。
なお、スクリプトの設計としては、先ず全ての玉に1を入れて、そのうち一つの玉の数を1ずつ増やしていき適当な数で繰り上げ、増やすたびに条件に合うかどうか調べるようなものの方が簡単かつ簡潔に書けますが、処理速度は牛歩に等しいです。
何時の間にか11月ももう下旬に入ろうとしていますが、如何お過ごしでしょうか。
……9月にⅢ章いけるかも、なんて言っていたのがつい昨日のことのように思えます。光陰矢のごとしとは良く言ったものですね。
いい加減充電期間も終わらせなければ。
さて、今日の話題は3回前に投稿したビリヤードの玉の問題についてです。
皆さん解けましたか?
以下一部解法に触れますので、自力で解きたい方はご注意ください。
一先ず問題を再掲しておきます。
『五つのビリヤードの玉を、真珠のネックレスのように、リングにつなげてみるとしよう。玉には、それぞれナンバーが書いてあるな。さて、この五つの玉のうち、幾つ取っても良いが、隣どうし連続したものしか取れないとしよう。一つでも、二つでも、五つ全部でも良い。しかし、離れているものは取れない。この条件で取った玉のナンバーを足し合わせて、1から21までのすべての数ができるようにしたい。さあ、どのナンバーの玉をどのように並べて、ネックレスを作れば良いかな?』
(森博嗣『笑わない数学者』より抜粋)
この問題を考察する上での肝は、21という数字が何処から出てきたかということにあるのですが、此処を乗り越えてしまえば球の個数が5個の場合に限らず、n個の場合に拡張して考えることも比較的容易にできます。
そうは言っても答えが規則的に現れる訳ではないので、同じ考え方が使えると言うだけですが、同じ考え方が使えるということは、機械的に解法をプログラムできるということになります。
そんな訳で例によってRGSSで手慰みに書いてみたのですが、それを出す前に先ず21の持つ意味を説明しますと、これは5個の玉の取り方の数になります。
取る玉の数1~4個に対して、取り始める点が5か所ずつ、それに全て取った場合の1通りを加えて 4*5+1=21 通りですね。
n個に拡張した場合は n(n-1)+1 通りになります。
また、これは全ての取り方に於いて球の数の和に重複は存在しないことを示しています。
例えば1と2の玉が隣り合っていたら、3の玉は絶対に入りません。
更にこのことを考えれば、1~21の全ての数を作るという条件を、5つの玉の数の総和が21かつ全ての取り方に於いて和に重複が無い、と言い変えることができます。
こうすることで条件の一致不一致を素早く判別することができます。
以上のことを考察した上で解法をスクリプトにしてみました。興味のある方はご覧下さい。
billiards.txt
さて、これを使って計算してみると答えの個数について面白い事実が浮かび上がって来ます。
球の個数が4個の時に二つ答えが出るのは人が考えても直ぐに分かりますが、6個にすると答えは五つに増え、更に7個にすると今度は答えは存在しないのです。
球の個数が1個の時から答えの数を並べると
1→1→1→2→1→5→0→6→4→6→0→18→……
となります。
今ブログを書いているPC環境では、12個の場合を計算するのに3,4分掛かったので、これ以上は面倒で計算してませんが、こういった規則性の無さにも数字の醍醐味を感じますね。
なお、スクリプトの設計としては、先ず全ての玉に1を入れて、そのうち一つの玉の数を1ずつ増やしていき適当な数で繰り上げ、増やすたびに条件に合うかどうか調べるようなものの方が簡単かつ簡潔に書けますが、処理速度は牛歩に等しいです。
DeJesusがOAKへトレードとなりました。
怪我で流れはしましたが、フラッグディールのほぼ確実視されていた選手ですから、格別の驚きはないのですが、ホームグロウン選手がチームを去るのは矢張り寂しいものです。
OAKはDeJesusを含めると外野手が余るので、この後更にトレードとなるかもしれませんが、何処へ行っても新天地で頑張ってほしいものです。
そんな訳で少々詩的な感傷に浸っているAlhenaです。秋ですしね。
そういえば一時期秋を飛ばして冬がやってきた、なんて騒がれましたが、少し時期を置いてみればなんてことのない普通の秋になっていますね。
何事も早計はいけません。
ところで一月ほど前にひっそりとカウンターを置いてみたのですがお気づきでしょうか。
以前自分で半分以上回しそうだ、なんて書きましたが、管理者は数えないように設定できたので、その心配は杞憂に終わりました。
しかしながら今現在38までしかカウントされていないので、私が週に3,4回は覗くことを考えると、設定できなければ危うい所だったとも言えます。
ふと思ったのですが、管理者に多重ログインって出来るのでしょうか。
アクセス解析はしていないので分かりませんが、出来ないのなら殆どをAbleが回している、なんて可能性も……。
怪我で流れはしましたが、フラッグディールのほぼ確実視されていた選手ですから、格別の驚きはないのですが、ホームグロウン選手がチームを去るのは矢張り寂しいものです。
OAKはDeJesusを含めると外野手が余るので、この後更にトレードとなるかもしれませんが、何処へ行っても新天地で頑張ってほしいものです。
そんな訳で少々詩的な感傷に浸っているAlhenaです。秋ですしね。
そういえば一時期秋を飛ばして冬がやってきた、なんて騒がれましたが、少し時期を置いてみればなんてことのない普通の秋になっていますね。
何事も早計はいけません。
ところで一月ほど前にひっそりとカウンターを置いてみたのですがお気づきでしょうか。
以前自分で半分以上回しそうだ、なんて書きましたが、管理者は数えないように設定できたので、その心配は杞憂に終わりました。
しかしながら今現在38までしかカウントされていないので、私が週に3,4回は覗くことを考えると、設定できなければ危うい所だったとも言えます。
ふと思ったのですが、管理者に多重ログインって出来るのでしょうか。
アクセス解析はしていないので分かりませんが、出来ないのなら殆どをAbleが回している、なんて可能性も……。
