月草色の幻影 Official Site

先日の嵐で秋も愈々終焉の様相を呈してきました。
週明けにはMLBのウィンターミーティングも始まりますし、私の最も好きな季節になろうとしています。

唯一の不満は野球がオフシーズンであることですが、youtubeのMLBチャンネルやMVPベースボールなどで無聊を慰めています。

皆さん今日は、Alhenaです。


先日今年の本屋大賞に選ばれた『天地明察』を友達に薦められたので読んでみました。
小説自体も流石に噂に違わぬ面白さだったのですが、私が注目したいのは例によって作中の問題についてです。

長さを長さで割っても面積を面積で割っても長さになるような明らかにおかしい誤問や、条件の通りに平均を出すとどう考えても絵に合わなくなる招差術の問題はどうでもいいのですが、気になったのは冒頭に登場する三角形と円の問題です。

先ずは問題を掲載しておきます。




上図のように直角三角形の中に直径の等しい二つの円が接している。
釣9寸、股12寸の時、円の直径を求めよ。



手元に本が無いので問題文は適当ですが、設問自体には影響ない筈です。
この問題を解くのに主人公は結構な苦労を強いられるのですが、実際解いてみるとさほど難しいとは感じないと思います。
ただし、小説の後半で登場人物の一人が代数を生みだしたという記述があるので、江戸時代初期当時の算術を考えればかなりの難問だったのかもしれません。

それは兎も角、この問題に対して主人公の出した答えは以下のようなものでした。

{2*釣*股/(釣+股+勾)}*{勾/(釣+股)}

この問題を初めて解いた時に、この式と一致する解法を採った方はいらっしゃるのでしょうか。
私の周囲では私を含め4人ほどこの問題に挑みましたが、皆この式で表される解法にはなりませんでした。
皆さんも是非試してみて下さい。



なのでどのような解法ならば過不足なくこの式に行き当たるかを私なりに考えてみました。



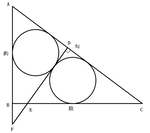
上図のように釣を延長し、二つの円の接点を通り勾に垂直な直線を引きます。
この時、⊿ADFと⊿EDCは、共に⊿ABCと相似なので相似であり、同じ半径の内接円を持っている為、合同になります。
従ってAD=EDですから、⊿ABCと⊿EDCの相似比は、
AB+BC : ED+DC = AB+BC : AD+DC = AB+BC : AC　　　となります。

ここで、⊿ABCの内接円の直径を考えると、2*{AB*BC/(AB+BC+CA)} ですから、答え、即ち⊿EDCの内接円の直径は次式で表されます。

{2*AB*BC/(AB+BC+CA)}*{AC/(AB+BC)}

一部形を合わせる為に手は加えていますが、これで主人公の式と一致しました。
彼の辿った解法はこのようなものだったのではないかと想像します。

以上、下らない妄想にお付き合い頂き有難う御座いました。